2020 H2 Math Paper 2 Full Solutions
When
When When Solving using a G.C.,
Equation of curve:
Equation of curve:
The sequence increases and diverges.
(B)
The sequence is a constant sequence for all
Using G.C., or
Since ,
At
Gradient of normal
Cartesian equation of :
Area of triangle
The curve cuts the -axis at
Area required
Replacing with
Cartesian equation of :
Differentiating w.r.t.
At maximum volume
Maximum volume
At maximum area
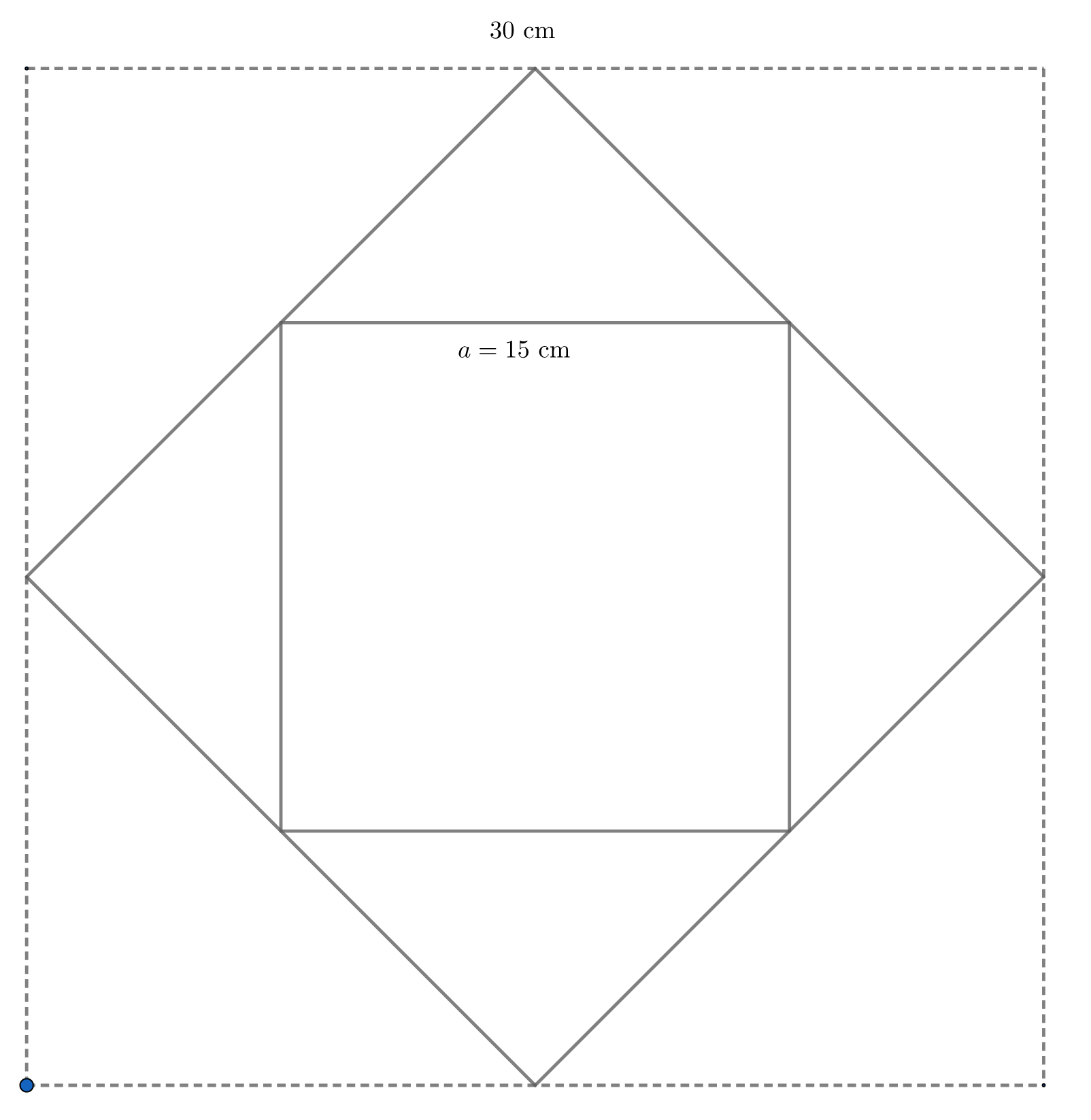 The net forms a square with sides
The net forms a square with sides Let denote
The probability distribution of is
The probability distribution of is
| 0 | 4 | 10 | 25 | |
The probability that James is late for work when he walks is (to 3 s.f.).
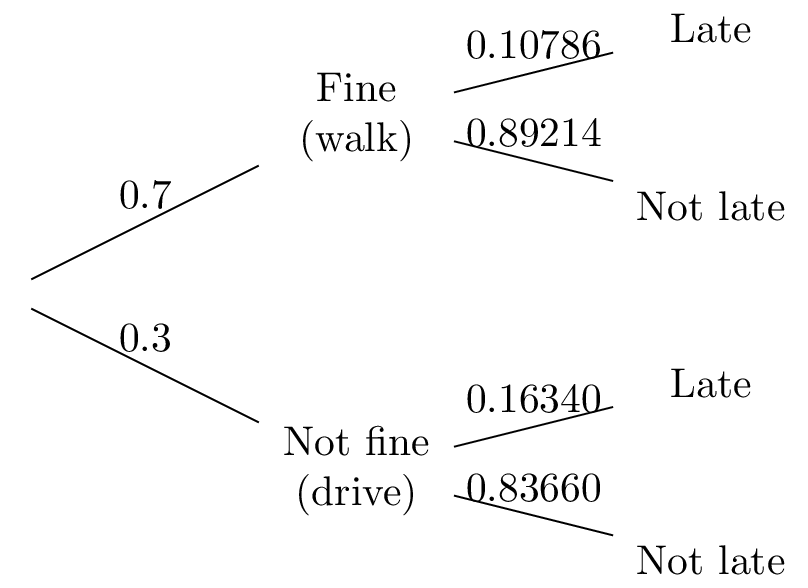
Hence
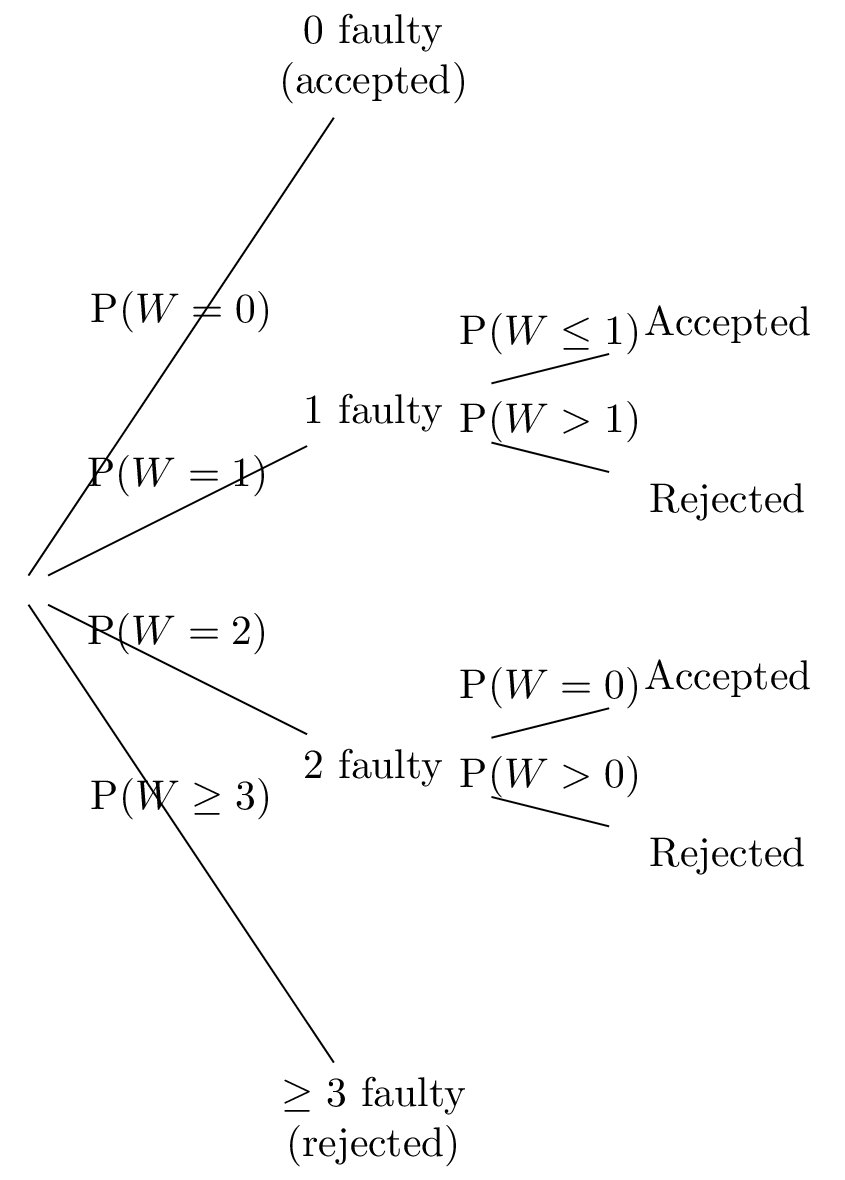
Under
Test statistic
For the critical region of the test at the 5% level of significance,
or
Critical region:
In the new test, we no longer know if the amount of carbon in each bar is normally distributed. Moreover, the population standard deviation is not know. Hence a large sample size of 40 ensures that the sample mean amount of carbon in each bar will be normally distributed approximately by the Central Limit Theorem.
Unbiased estimate of population variance
Unbiased estimate of population variance
Under
Test statistic
Hence there is sufficient evidence at the 2.5% level of significance to conclude that the mean amount of carbon in the flat bars is more than 0.25%.